Le triangle de Sierpiński des 6A et 6F

Qu'est-ce qu'une fractale ?

Une fractale est une forme géométrique qui se répète à l'identique quand zoome dans la figure. La forme répétée est le plus souvent une spirale imbriquée dans une autre, mais peut également être un triangle ou un hexagone.
On retrouve dans la nature des exemples de fractale, comme par exemple les nuages, les vagues, les amas d'étoiles ou des objets plus petits comme des choux romanesco, des fougères ou un flocon de neige.

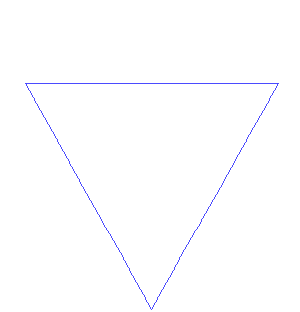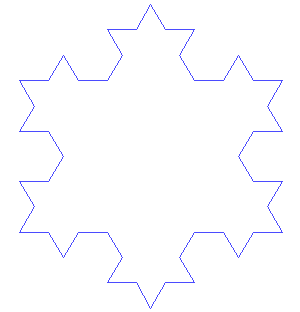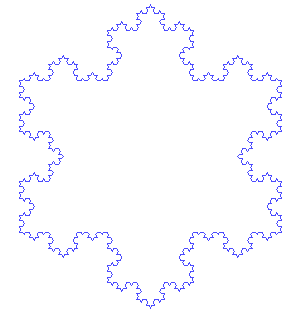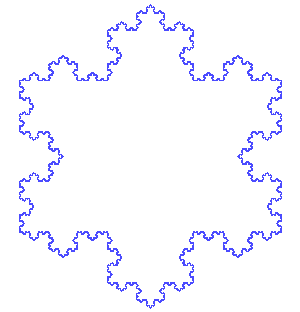
Comment est construite cette fractale collaborative ?

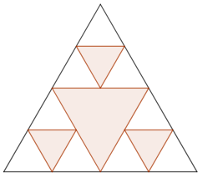Chaque élève a construit une petite partie de la figure, le motif réalisé est donné dans l'image ci-contre. Les différentes figures sont ensuite assemblées de manière aléatoire afin de former la fractale finale. La figure est construite avec Géogébra en ligne.

Pourquoi triangle de Sierpiński ?

Le triangle de Sierpiński est une fractale qui porte le nom de Wacław Sierpiński. C'est un mathématicien polonais né en 1882 et mort en 1969. Il a fait des recherches en mathématique sur des choses liées à cette fractale.
L'image ci-dessous montre les premières étapes de construction du triangle de Sierpiński.

Énigmes

Énigme n°1

Si 25 élèves participent à la figure collaborative, combien il y a-t-il de triangles colorés ?

Énigme n°2

À partir de la figure montrant les étapes de construction du triangle de Sierpiński (l'image juste au dessus), répondre aux questions suivantes :

1. Combien y a-t-il de triangles blancs à l'étape 1 ?
2. Combien y a-t-il de triangles blancs à l'étape 2 ?
3. Combien y a-t-il de triangles blancs à l'étape 3 ?
4. Plus dur, combien y a-t-il de triangles blancs à l'étape 5 ?
5. Encore plus dur. L'étape 7 est composé de 2187 triangles blancs. Combien de triangles blancs y a-t-il à l'étape 8 ?

Énigme n°3

Toujours à partir de la figure montrant les étapes de construction du triangle de Sierpiński. Si on considère que l'aire du triangle de l'étape 0 est de 1 unité d'aire. Quelle est l'aire (en blanc) de la figure à l'étape 1 ? à l'étape 2 ?